Hierarchical Clustering
5/4/23
Housekeeping
- Project drafts due Sunday!
- K-means implementation open today
- Due last day of classes (Monday, 5/15)
Hierarchical clustering
Motivation
Disadvantage of \(K\)-means is pre-specifying \(K\)!
What if we don’t want to commit to a single choice?
We will construct a (upside-down) tree-based representation of the observations dendrogram
Specifically focus on bottom-up hierarchical clustering, by constructing leaves first and then the trunk
- Intuition/idea: rather than clustering everything at beginning, why don’t we build iteratively
Example
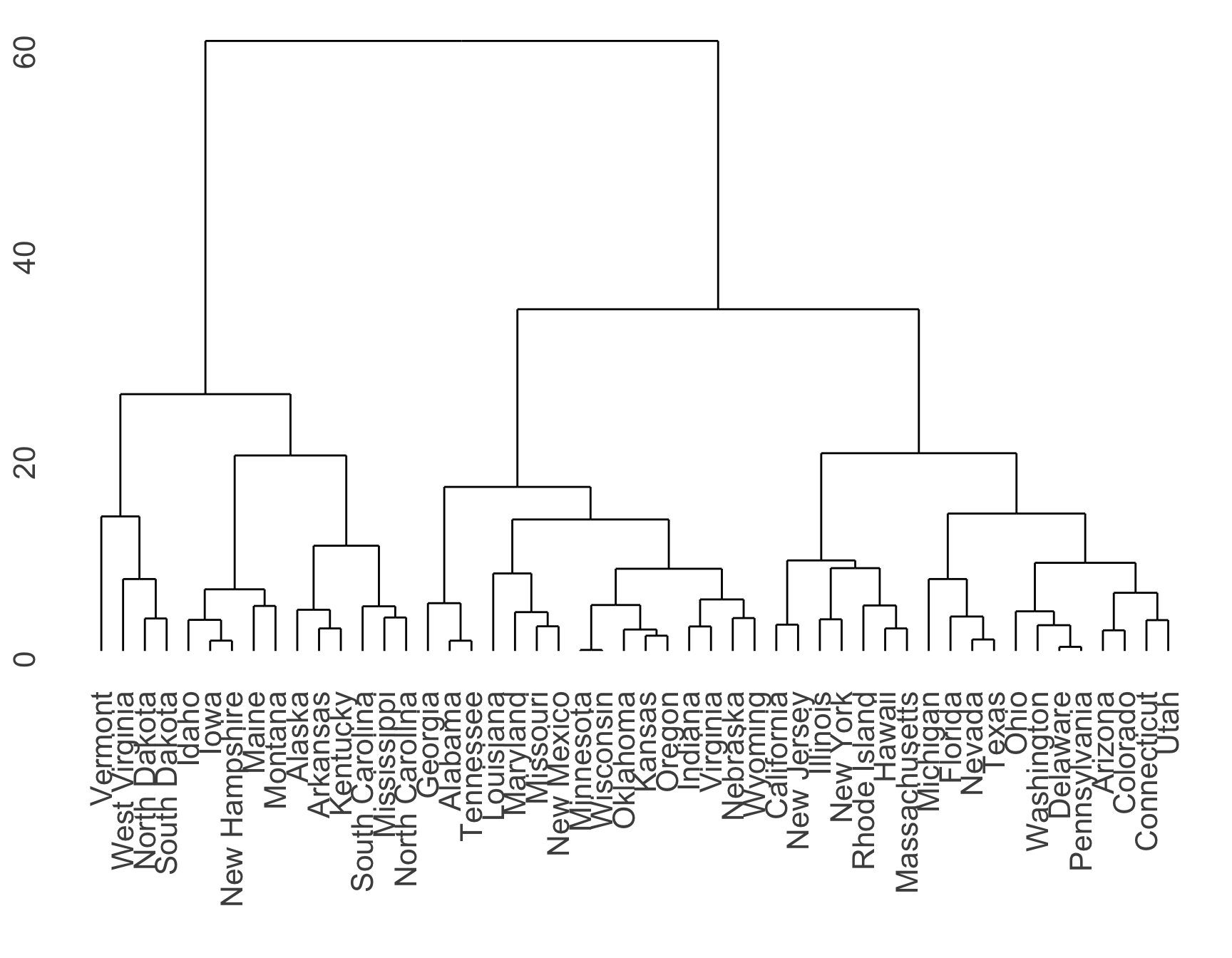
Dendrogram of hierarchically clustered USArrests data using number of Murder arrests (per 100,000) and percent urban population
“Algorithm”
The approach in words:
Start with each point in its own cluster
Identify the “closest” two clusters and merge them together
Repeat
Finish when all points have eventually been combined into a single cluster
Dendrogram
Each leaf of the dendrogram is one of the \(n\) observations
As we move up the tree, some leaves fuse into branches
- These correspond to observations that similar to each other
Branches and/or leaves will fuse as we move up the tree
The earlier (lower in the tree) fusions occur, the more similar the groups
For any two observations, look for the point in tree where branches containing these two observations are first fused
The height of this fusion on vertical axis indicates how different they are
Caution! Cannot draw conclusions about similar based on proximity of observations on the horizontal axis
- Why?
Identifying clusters
To identify clusters based on dendrogram, simply make a horizontal cut across dendrogram
Distinct sets of observations beneath the cut are interpreted as clusters
This makes hierarchical clustering attractive: one single dendrogram can be used to obtain any number of clusters
- What do people do in practice?
“Hierarchical”
Clusters obtained by cutting at a given height are nested within the clusters obtained by cutting at any greater height
Is this realistic?
More rigorous algorithm
Need to define some sort of dissimilarity measure between pairs of observations (e.g. Euclidean distance)
Begin with \(n\) observations and a measure of all the \(\binom{n}{2}\) pairwise dissimilarities. Treat each observation as its own cluster.
For \(i = n, n-1, n-2,\ldots, 2\):
Examine all pairwise inter-cluster dissimilarities among the \(i\) clusters and identify the pair of clusters that are least dissimilar. Fuse these two clusters. Their dissimiliarity is the height in the dendrogram where the fusion should be placed.
Compute the new pairwise inter-cluster dissimilarities among the remaining \(i-1\) remaining clusters
Dissimilarity between groups
How do we define dissimilarity between two clusters if one or both contains multiple observations?
- i.e. How did we determine that \(\{A,C\}\) should be fused with \(\{B\}\)?
Develop the notion of linkage, which defines dissimilarity between two groups of observations
Common linkage types
Complete: maximal intercluster dissimilarity. Compute all pairwise dissimilarities between observations in cluster \(A\) and observations in cluster \(B\). Record the largest of these dissimilarities.
Single: minimal intercluster dissimilarity. Compute all pairwise dissimilarities between observations in cluster \(A\) and observations in cluster \(B\). Record the smallest of these dissimilarities.
Average: mean intercluster dissimilarity. Compute all pairwise dissimilarities between observations in cluster \(A\) and observations in cluster \(B\). Record the average of these dissimilarities.
Centroid: dissimilarity between the centroid for cluster \(A\) and the centroid for cluster \(B\)
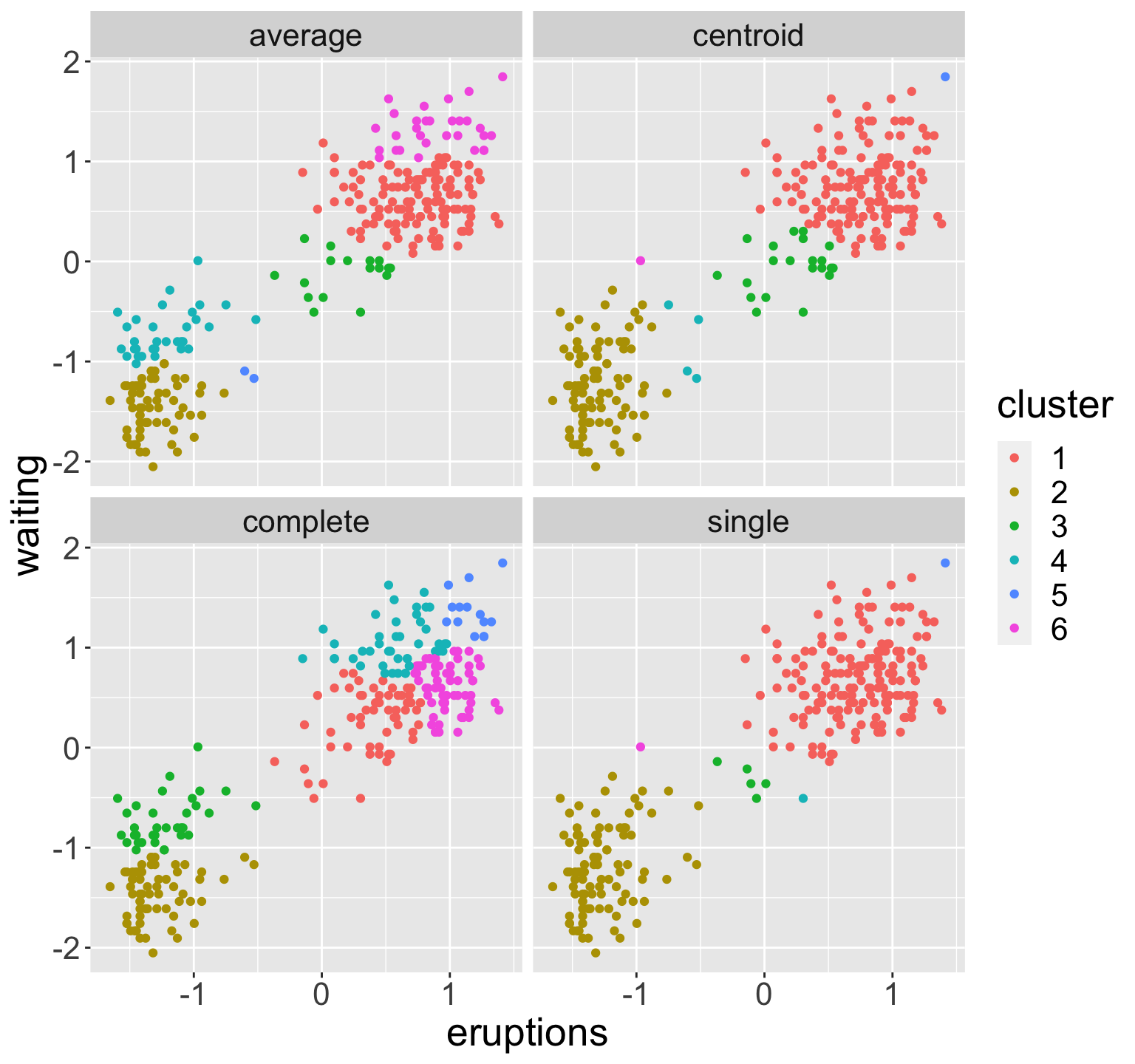
Example: old faithful
faithful data: waiting time between eruptions and the duration of the eruption for the Old Faithful geyser in Yellowstone National Park, Wyoming, USA.
Two features (standardized): eruption and waiting times
Hierarchical clustering using all four linkage types
In each case, performed clustering and then cut to obtain six groups
Choice of linkage
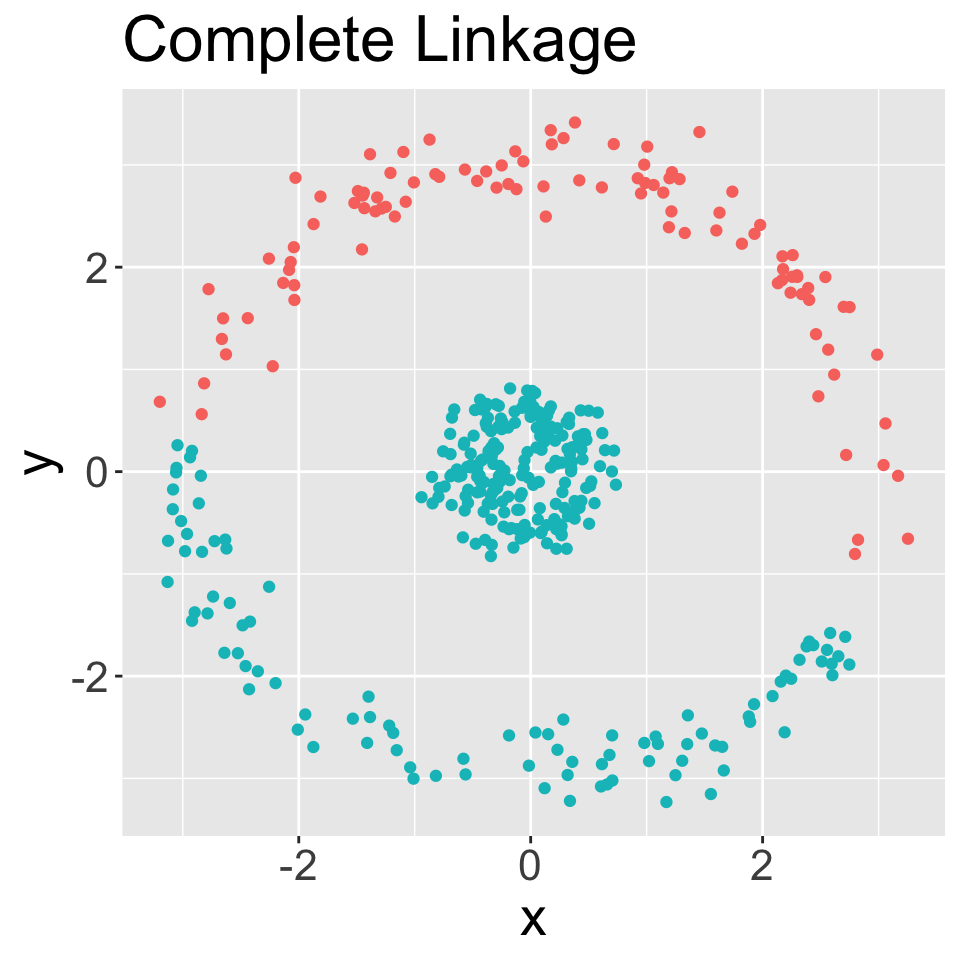
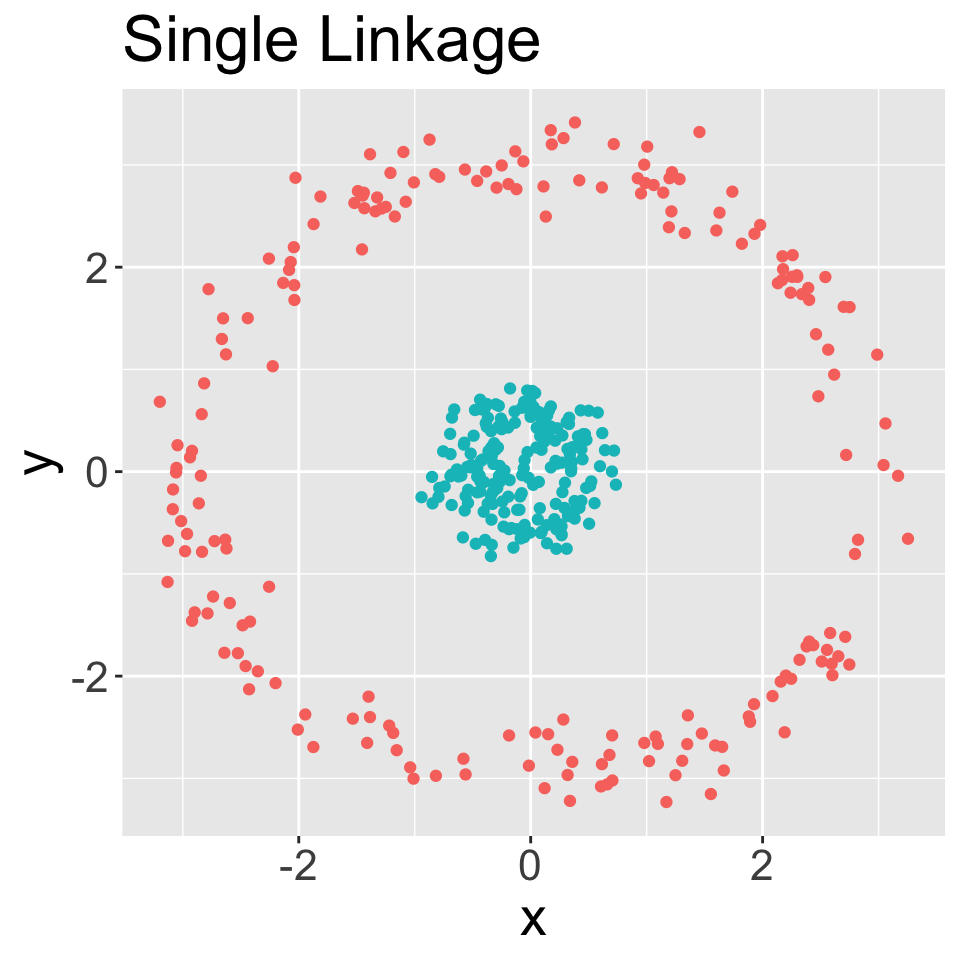
Average and complete are generally preferred over single linkage
- Tend to yield more balanced dendrograms
Centroid linkage often used in genomics
- Drawback of inversion, where two clusters are fused at a height below either of the individual clusters
Your turn!
Summary
Decisions
Should the features be standardized?
What dissimilarity measured should we use?
What type of linkage should we use?
Where should we cut the dendrogram?
Considerations
How do we validate the clusters we obtained?
- Are we truly discovering subgroups, or are we simply clustering the noise?
Do all observations belong in a cluster? Or are some actually “outliers”
Clustering methods generally not robust to small changes in data
Live code
Examples
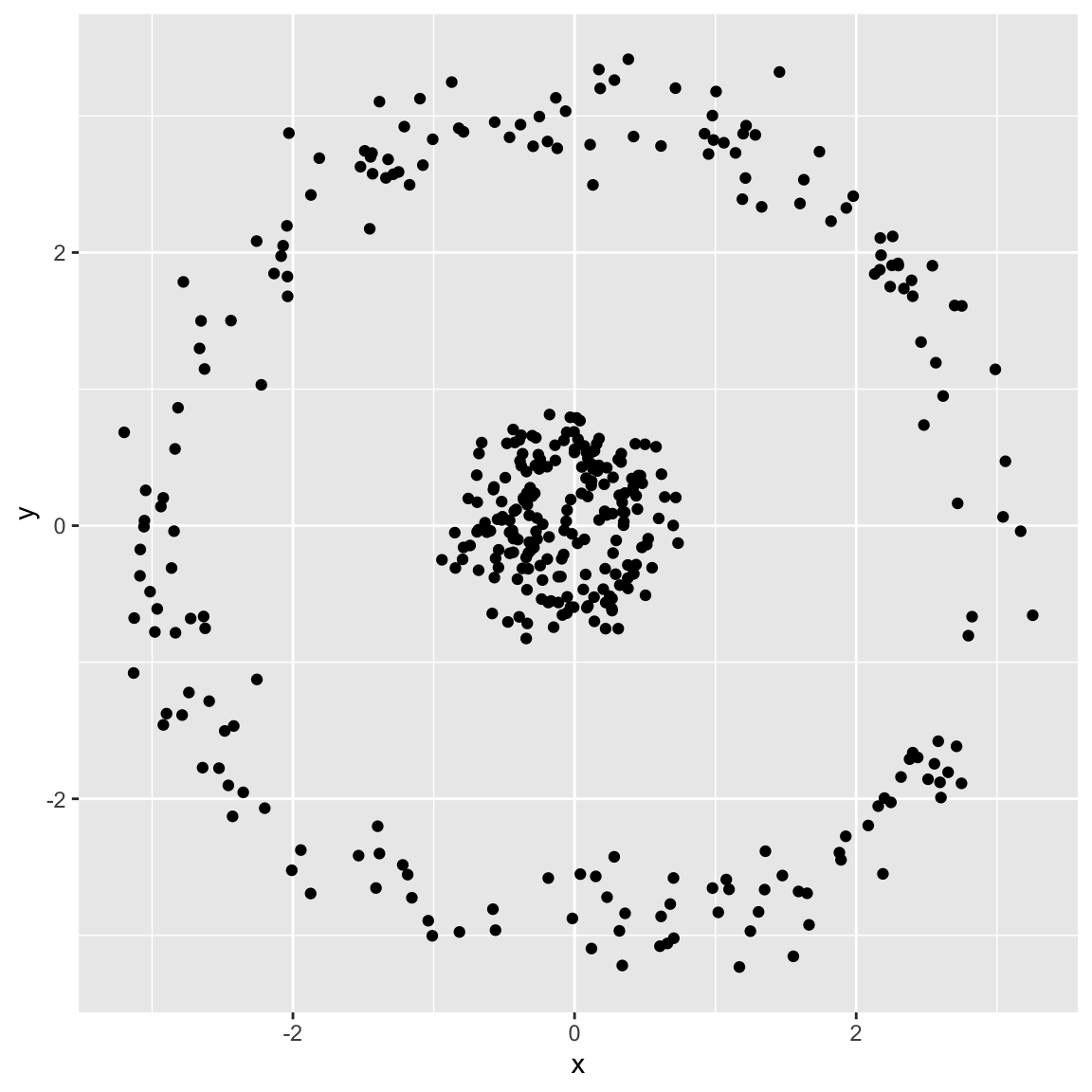
Spherical data
Generated the following data: