Classification Trees

Coding

4/20/23

Housekeeping

  • Lab 05 due this tonight!
  • Project proposals due this Sunday to Canvas!

Image from Wikipedia

Coding classification trees

Copy and paste this code if you’d like to follow along!

obesity <- read.csv("https://raw.githubusercontent.com/math218-spring2023/class-data/main/obesity.csv")

Framing the data we are working with

We have data on obesity levels based on eating habits and physical condition in individuals from Colombia, Peru and Mexico (although some of this data is actually synthetic (i.e. fake)!).

  • I want to be clear that discussion about weight can be triggering and difficult for some people

  • I would like to frame this analysis by noting that weight is just one characteristic that scientists and doctors have used to represent health status, but it does not define health

Data

          class   n
1  Insufficient 272
2        Normal 287
3       Obese_I 351
4      Obese_II 297
5     Obese_III 324
6  Overweight_I 290
7 Overweight_II 290

  • Variables include: gender, age, smoke status, family history, amount of physical activity, etc.

  • Can we predict the obesity status based on these variables using decision trees? What variables might be important for classifying the status?

Analysis

  • Split data into 80% train, 20% test

  • Fit three different models to the data and obtained predictions for the test data:

    1. Pruned classification tree fit on the 80% train

    2. Bagged classification trees fit on all the data, but predictions obtained from OOB samples (B = 100 trees)

    3. Random forest classification fit on all the data, but predictions obtained from OOB samples (B = 100 trees)

Classification Tree

obesity_tree <- tree(class ~ ., data = train_dat,
                       control = tree.control(nobs = nrow(train_dat), minsize = 2))
cv_tree <- cv.tree(obesity_tree, FUN = prune.misclass)
best_size <- min(cv_tree$size[which(cv_tree$dev == min(cv_tree$dev))])
prune_obesity <- prune.misclass(obesity_tree, best = best_size)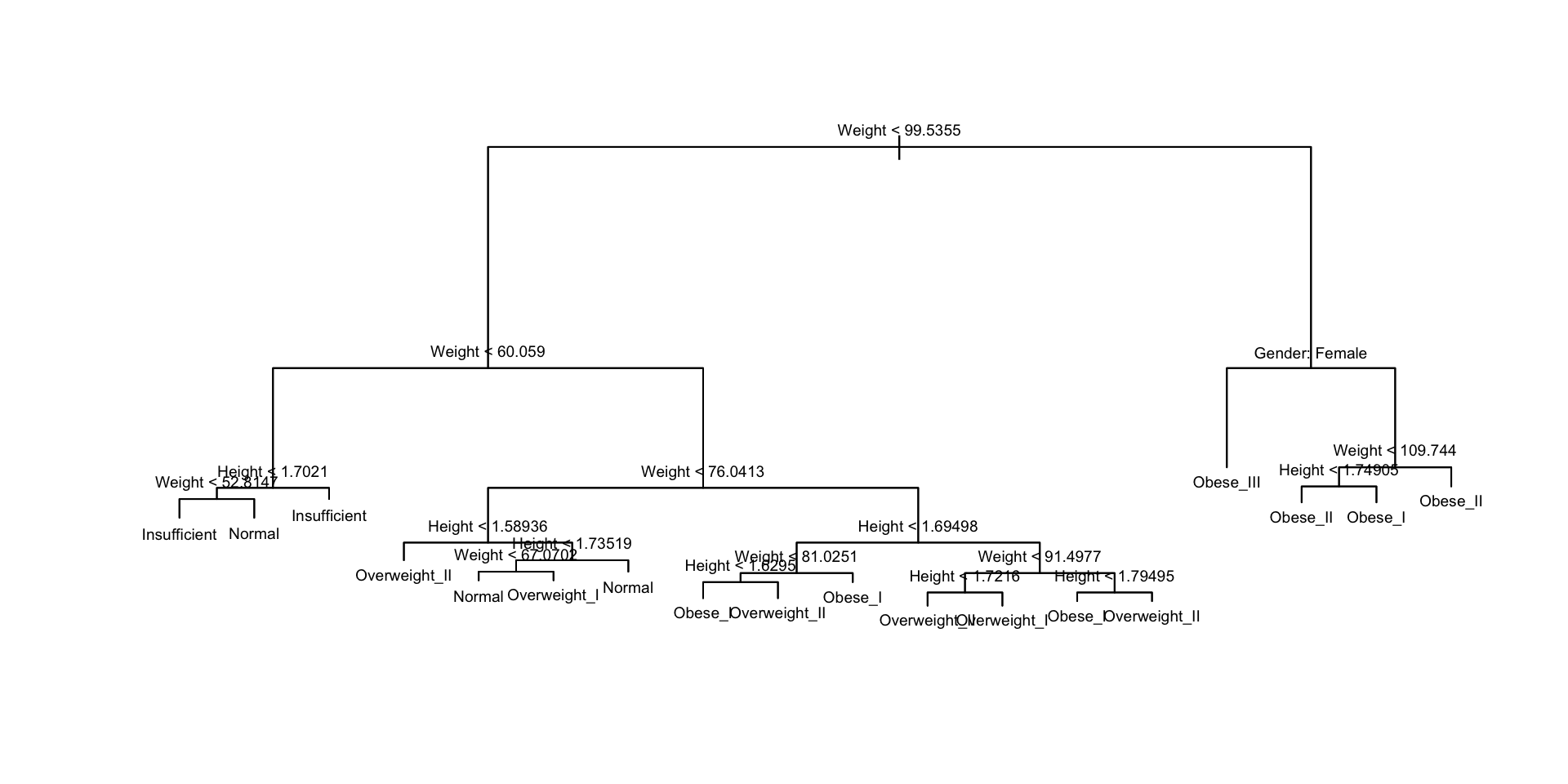

Classification Tree: predictions

Use the predict() function like usual to obtain predictions:

head(predict(prune_obesity, newdata = test_dat))
   Insufficient   Normal  Obese_I Obese_II Obese_III Overweight_I Overweight_II
3      0.000000 0.093960 0.000000 0.000000         0     0.530201      0.375839
4      0.000000 0.093960 0.000000 0.000000         0     0.530201      0.375839
6      0.011905 0.892857 0.000000 0.000000         0     0.095238      0.000000
10     0.000000 0.113821 0.000000 0.000000         0     0.853659      0.032520
18     0.000000 0.000000 1.000000 0.000000         0     0.000000      0.000000
24     0.000000 0.000000 0.951923 0.028846         0     0.000000      0.019231
  • Is this what we wanted?
head(predict(prune_obesity, newdata = test_dat, type = "class"))
[1] Overweight_I Overweight_I Normal       Overweight_I Obese_I     
[6] Obese_I     
7 Levels: Insufficient Normal Obese_I Obese_II Obese_III ... Overweight_II
  • What’s our misclassification rate?
[1] "Misclass rate: 0.158"

Bagged classification trees

Quickly discuss/remind ourselves: what does bagging for trees look like?

obesity_bag <- randomForest(class ~ ., data = obesity, ntree = 100,
             mtry = ncol(obesity) - 1)
varImpPlot(obesity_bag)

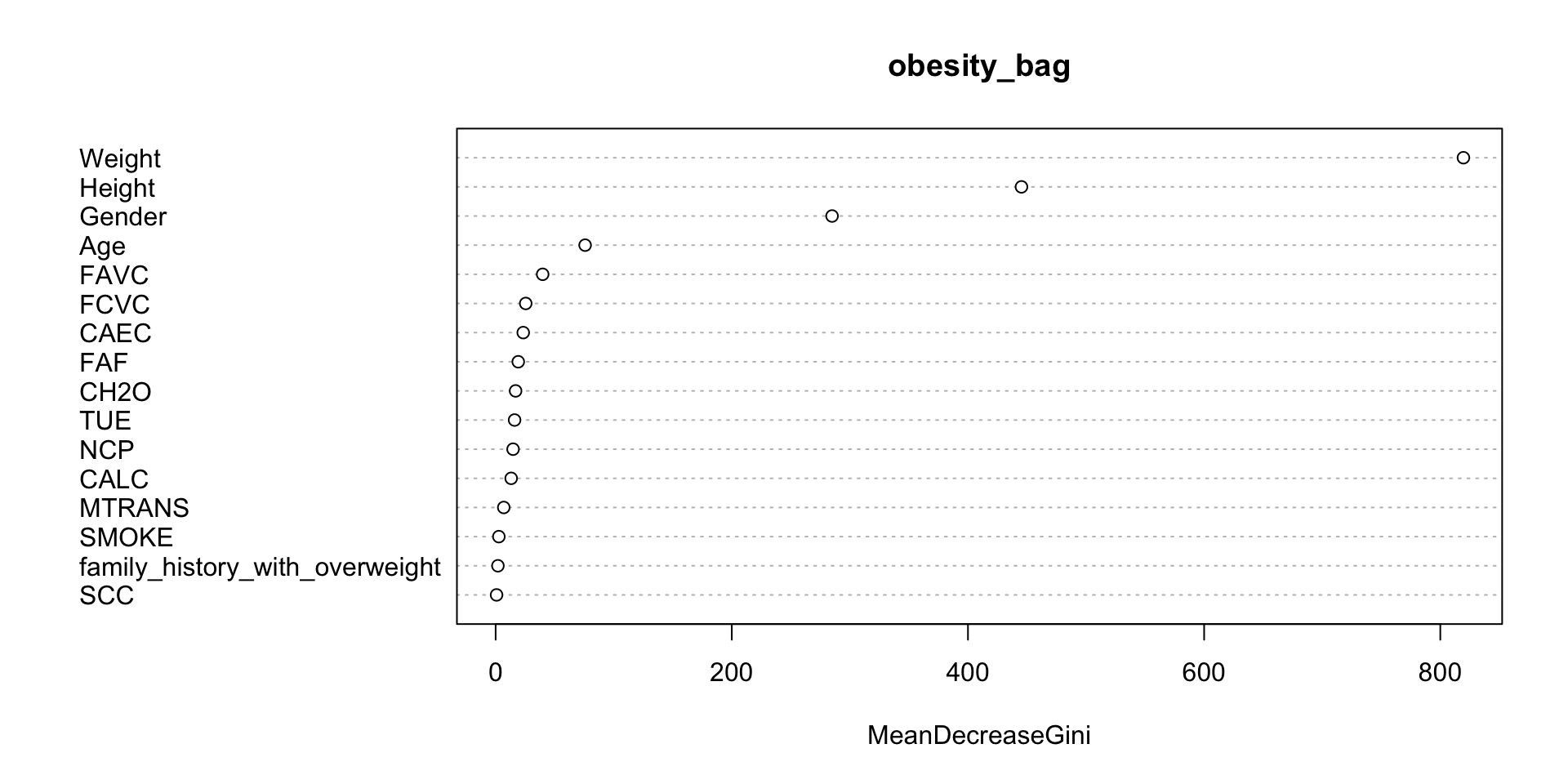
  • The “importance” is defined as the total amount that the Gini index decreases by splits over a given predictor \(X_{j}\), averaged over the \(B\) trees

Aggregating predictions

  • Discuss: how does a bagged model predict a single class across \(B\) different trees?

    • i.e. What does it mean to aggregate multiple labels?

  • For a given test point, each tree will output a predicted label \(\hat{y}^{(b)}\). We will take a majority vote approach again!

    • The overall prediction for a test point is the most commonly occurring label among the \(B\) predictions
[1] "Misclass rate: 0.026"

Random forests

For random forests, we typically set the number of predictors to consider at each split to be \(\approx \sqrt{p}\), where \(p\) is the total number of available predictors

[1] "Misclass rate: 0.05"

Comparing all models

Which model would we prefer?

          model error_rate
1   Pruned tree 0.15839243
2        Bagged 0.02600473
3 Random Forest 0.04964539