Model Assessment and KNN Classification

4/6/23

Housekeeping

• We will have an implementation assignment this week (most likely begin in class tomorrow)

• Still need to hear about project partners!

Model assessment

Model assessment in classification

In the case of binary response, it is common to create a confusion matrix, from which we can obtain the misclassification rate and other rates of interest

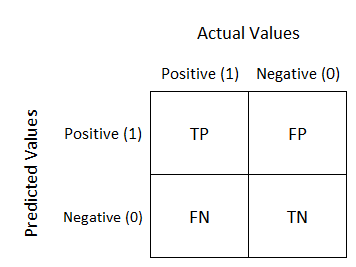
• FP = “false positive”, FN = “false negative”, TP = “true positive, TN =”true negative

  • “Success” class is the same as “positive” is the same as “1”

• Can calculate the overall error/misclassification rate: the proportion of observations that we misclassified

  • Misclassification rate = \(\frac{\text{FP} + \text{FN}}{\text{TP} + \text{FP} + \text{FN} + \text{TN}} = \frac{\text{FP} + \text{FN}}{n}\)

Example

pred	true
0	0
1	1
0	1
1	0
1	1
1	1
0	0
0	0
1	1
0	1

• 10 observations, with true class and predicted class

• Make a confusion matrix!

Pred	True
	0	1
0	3	2
1	1	4

Types of errors

• False positive rate (FPR): fraction of negative observations incorrectly classified as positive

  • Number of failures/negatives in data = \(\text{FP} + \text{TN}\)

  • \(\text{FPR} = \frac{\text{FP}}{\text{FP} + \text{TN}}\)

• False negative rate (FNR): fraction of positive observations incorrectly classified as negative example

  • Number of success/positives in data = \(\text{FN} + \text{TP}\)

  • \(\text{FNR} = \frac{\text{FN}}{\text{FN} + \text{TP}}\)

Mite data errors

I fit a logistic regression to predict heart present using predictors Topo and WatrCont, and obtained the following confusion matrix of the train data:

mite_log <- glm(present ~ Topo + WatrCont, data = presence_dat,family = "binomial")

Pred	True
	0	1
0	16	5
1	5	44

• What is the misclassification rate?

  • Misclassification rate: (5 + 5)/70 = 0.143

• What is the FNR? What is the FPR?

  • FNR: 5/49 = 0.238

  • FPR: 5/21 = 0.102

Threshold

• Is a false positive or a false negative worse? Depends on the context!

• The previous confusion matrix was produced by classifying an observation as present if \(\hat{p}(x)=\widehat{\text{Pr}}(\text{present = 1} | \text{Topo, WatrCont}) \geq 0.5\)

  • Here, 0.5 is the threshold for assigning an observation to the “present” class

  • Can change threshold to any value in \([0,1]\), which will affect resulting error rates

Varying threshold

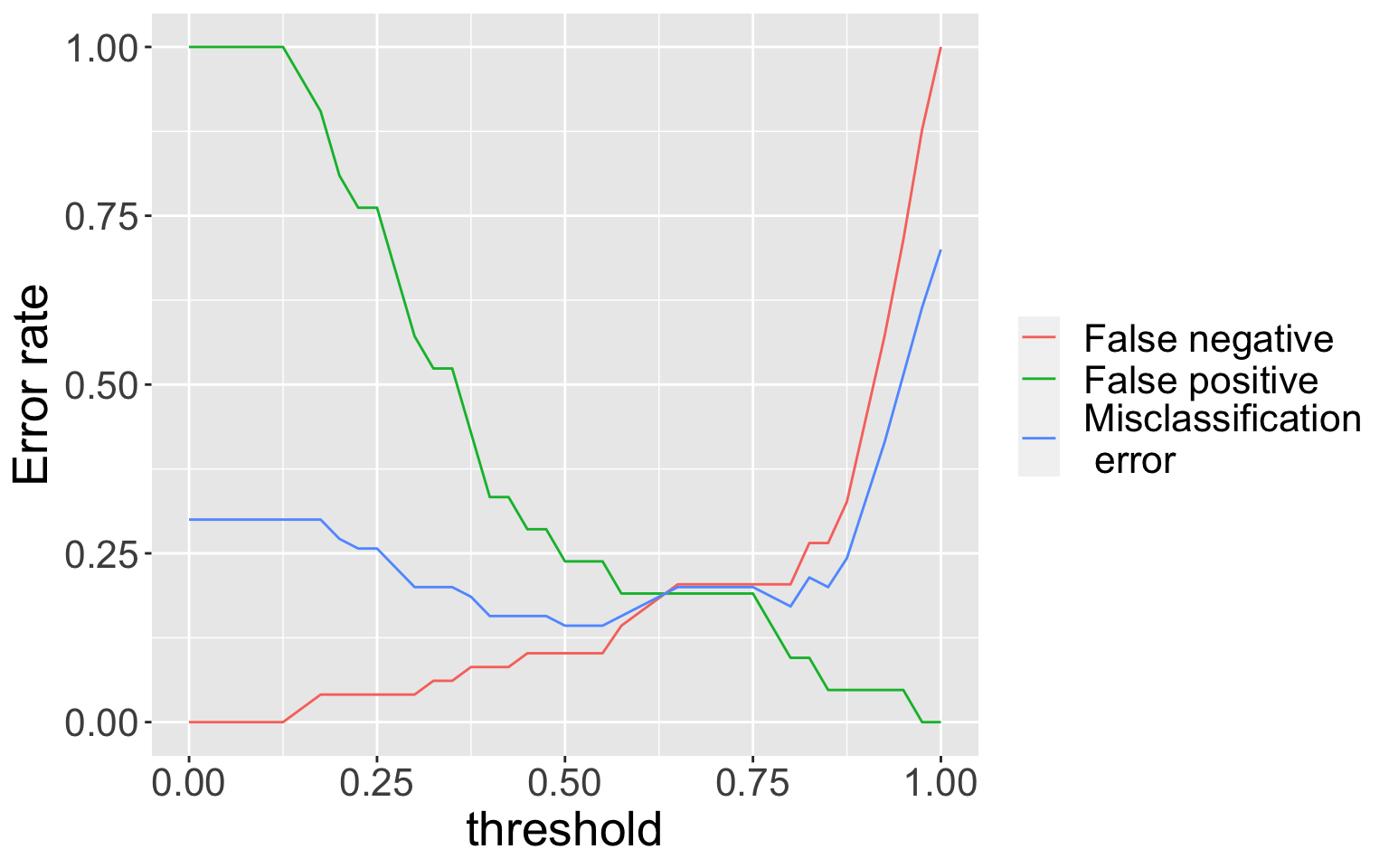
• Overall error rate minimized at threshold near 0.50

• How to decide a threshold rate? Is there a way to obtain a “threshold-free” version of model performance?

ROC Curve

• The ROC curve is a measure of performance for binary classification at various thresholds

  • ROC is a probability curve, and the Area under the curve (AUC) tells us how good the model is at distinguishing between/separating the two classes

• The ROC curve simultaneously plots the true positive rate TPR on the y-axis against the false positive rate FPR on the x-axis

• An excellent model has AUC near 1 (i.e. near perfect separability), whereas a terrible model has AUC near 0 (always predicts the wrong class)

  • When AUC = 0.5, the model has no ability to separate classes

ROC Curve (cont.)

ROC and AUC for the training data:

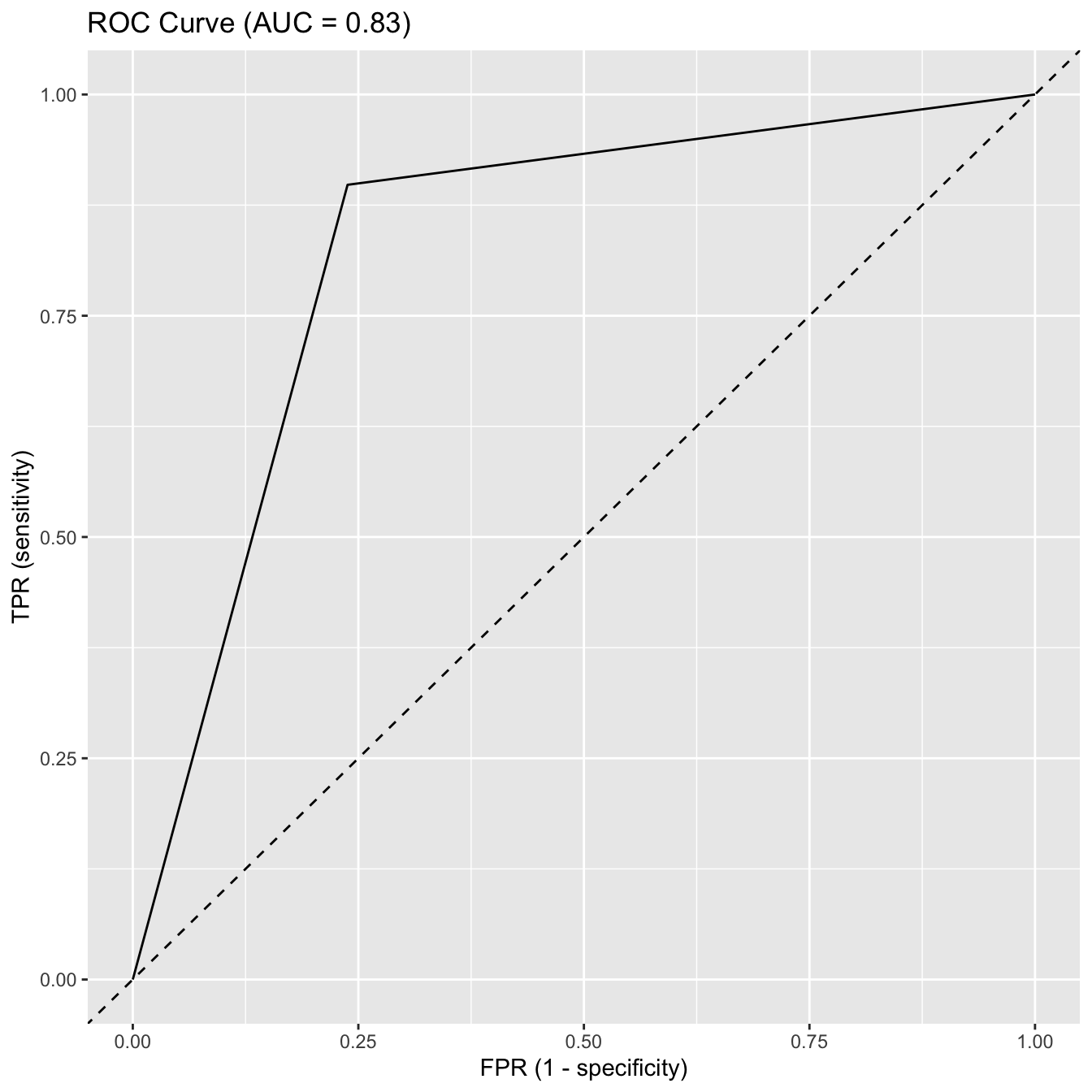
• How do you think we did?

KNN Classification

KNN Classification

• While logistic regression is nice (and still frequently used), the basic model only accommodates binary responses. What if we have a response with more than two classes?

• We will now see how we can use KNN for classification

  • Side note: when people refer to KNN, they almost always refer to KNN classification

• Finding the neighbor sets proceeds exactly the same as in KNN regression! The difference lies in how we predict \(\hat{y}\)

Example: mite data

• This is a similar plot to that from KNN regression slides, where now points (plotted in standardized predictor space) are colored by present status instead of abundance.

• Two test points, which we’d like to classify using KNN with \(K = 3\)

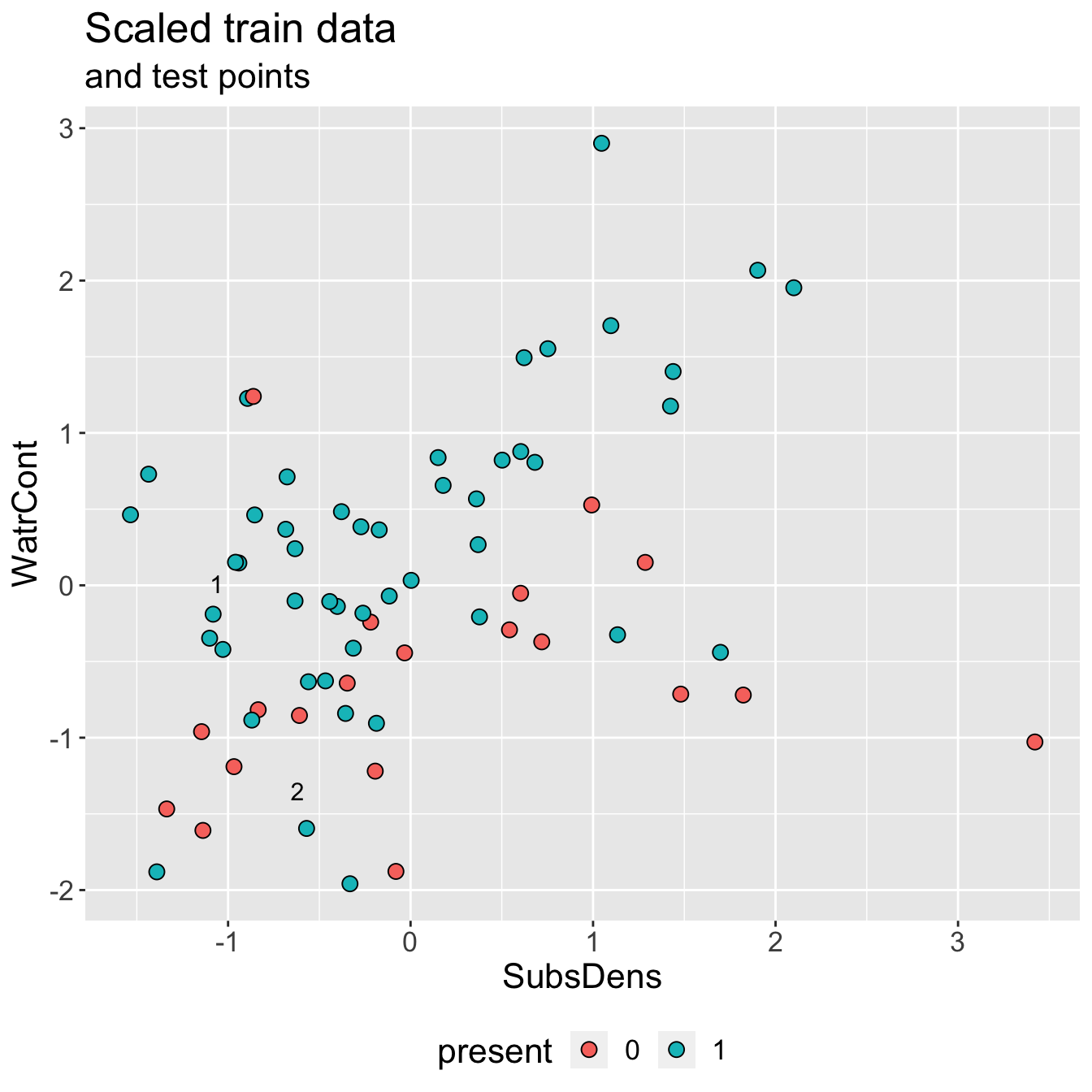
How would we classify?

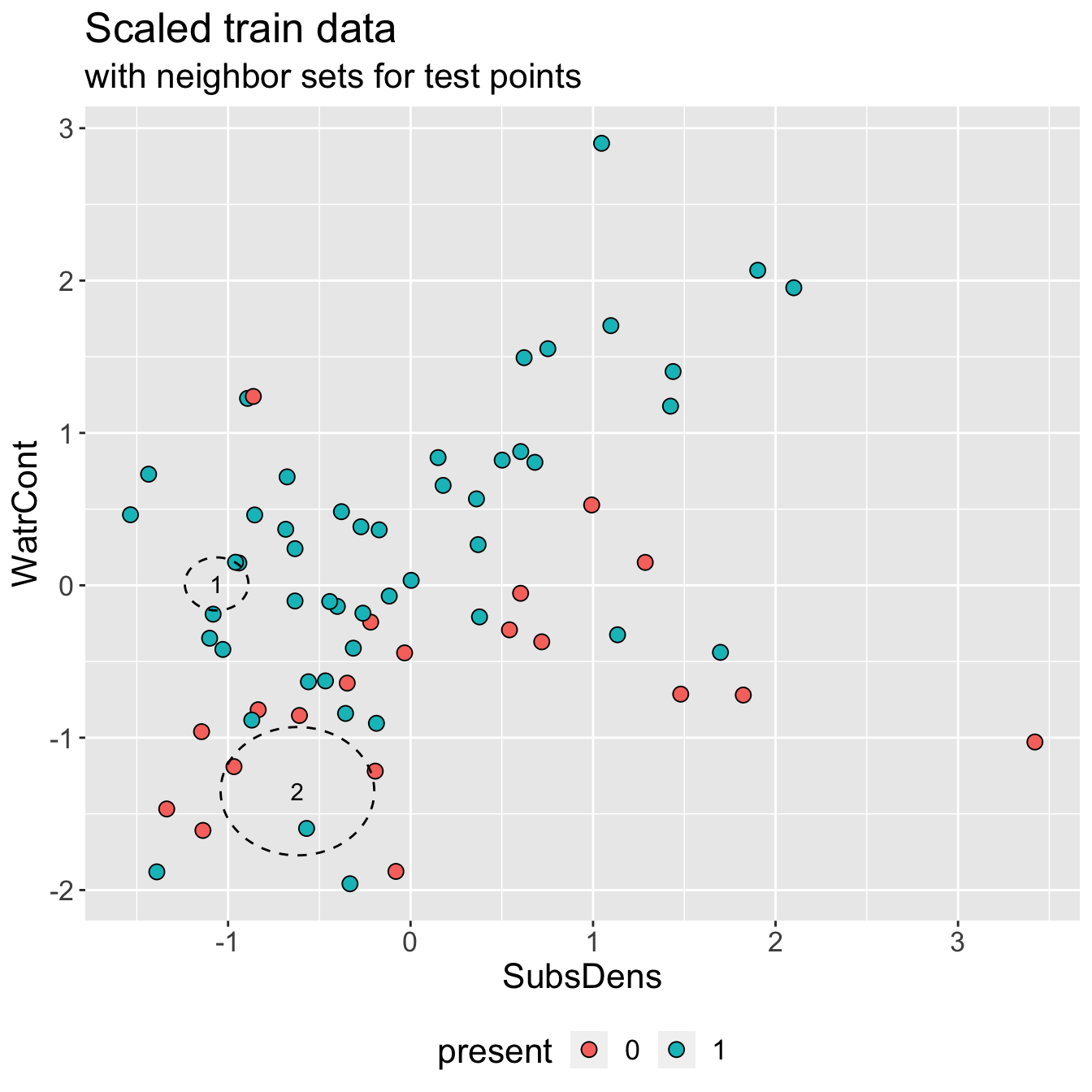
Discuss: which class labels would you predict for test points 1 and 2, and why?

• Estimated conditional class probabilities \(\hat{p}_{ij}(\mathbf{x}_{i})\) are obtained via simple “majority vote”:
  • \(\hat{p}_{1, \text{present}}(\mathbf{x}_{1}) = \frac{3}{3} = 1\) and \(\hat{p}_{1, \text{absent}}(\mathbf{x}_{1}) = \frac{0}{3} = 0\)
  • \(\hat{p}_{2, \text{present}}(\mathbf{x}_{2}) = \frac{1}{3}\) and \(\hat{p}_{2, \text{absent}}(\mathbf{x}_{2}) = \frac{2}{3}\)

Beyond two classes

• KNN classification is easily extended to more than two classes!

• We still follow the majority vote approach: simply predict the class that has the highest representation in the neighbor set

• palmerPenguins data: size measurements for adult foraging Adélie, Chinstrap, and Gentoo penguins

• We will classify penguin species by size measurements!

KNN classification: different K

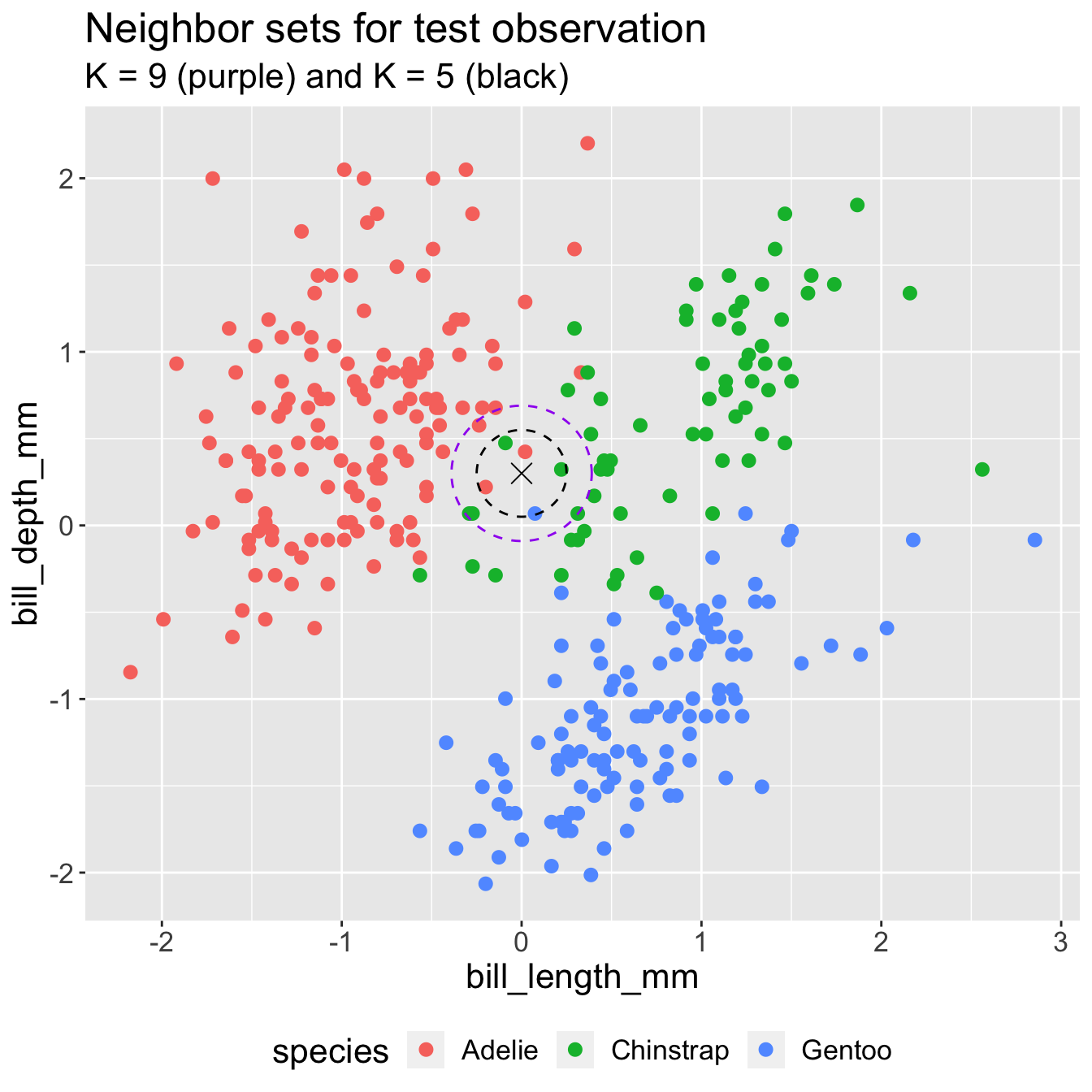
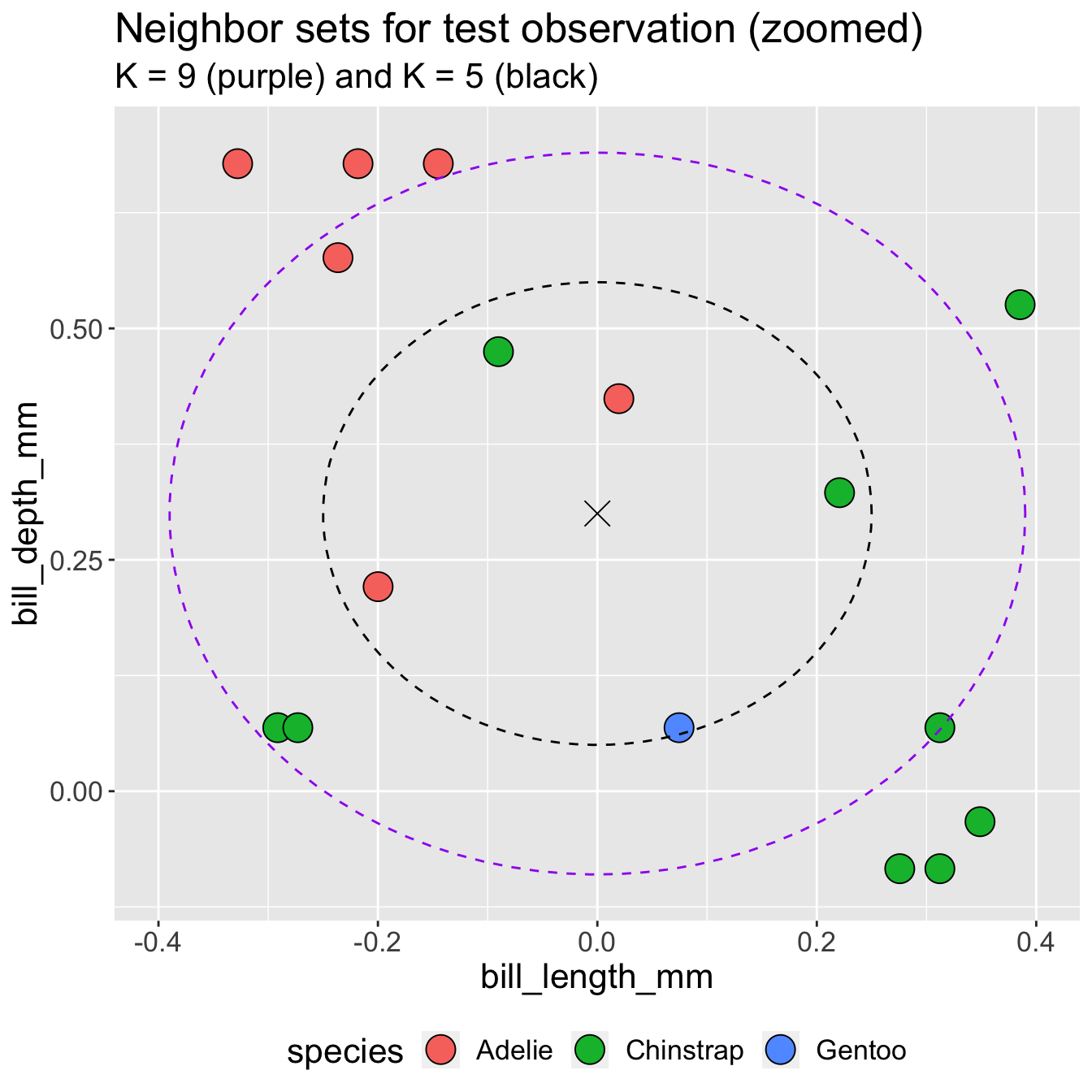
• What class would you predict for the test point when \(K = 9\)?
• What class would you predict for the test point when \(K = 5\)?

Handling ties

• An issue we may encounter in KNN classification is a tie

  • It is possible that no single class is a majority!

• Discuss: how would you handle ties in the neighbor set?