Bootstrap

3/28/23

Housekeeping

• Lab 04: Forest Fires due to Canvas this Thursday 11:59pm

• Lab 03 should be graded by end of today!

• Take-home midterm assigned this Friday (will introduce it today)

Resampling

• Economically use a collected dataset by repeatedly drawing samples from the same training dataset and fitting a model of interest on each sample

  • Obtain additional information about the fitted model

• Two methods: cross-validation and the bootstrap

• These slides will focus on the bootstrap

The Bootstrap

The Bootstrap

• The bootstrap is a flexible and powerful statistical tool that can be used to quantify the uncertainty associated with a given estimator or statistical learning method

• Example: can be used to estimate the standard errors of the \(\beta\) coefficients in linear regression

• One goal of statistics: learn about a population.

  • Usually, population is not available, so must make inference from sample data

• Bootstrapping operates by resampling this sample data to create many simulated samples

The Bootstrap (cont.)

• Bootstrapping resamples the original dataset with replacement

• If the original dataset has \(n\) observations, then each bootstrap/resampled dataset also has \(n\) observations

  • Each observation has equal probability of being included in the resampled dataset
  • Can select an observation more than once for a resampled dataset

Example: M&Ms

• Suppose I want to know the true proportion of plain M&M candies that are colored red

• My sample is a bag of M&Ms that I purchased at a gas station, which contains 56 pieces with the following distribution:

 [1] orange orange yellow red    blue   red    red    green  green  blue  
[11] blue   blue   green  orange brown  orange green  red    orange brown 
[21] red    blue   green  blue   orange orange blue   orange brown  orange
[31] orange yellow orange blue   brown  green  brown  blue   green  orange
[41] brown  green  brown  yellow yellow brown  blue   orange green  green 
[51] orange brown  orange blue   blue   blue  
Levels: red orange yellow green blue brown

obs
   red orange yellow  green   blue  brown 
     5     15      4     10     13      9 

• Good first guess for the true proportion of red candies?

  • 5/56 = 0.089

• How would we go about creating a range of plausible estimates? We could bootstrap!

Example: M&Ms (cont.)

• To obtain a single bootstrap sample, we repeatedly pull out an M&M, note its color, and return it to the bag until we have pulled out a total of \(n = 56\) candies

• We typically repeat this process many times, to simulate taking multiple observations from the population

Step-through code

• Create my first bootstrap sample:

n <- length(obs)
samp1 <- sample(x = obs, size = n, replace = T)
samp1

 [1] blue   red    green  orange green  red    blue   yellow orange orange
[11] yellow red    blue   orange blue   orange orange orange orange red   
[21] green  yellow red    orange green  blue   green  green  green  orange
[31] orange orange orange green  brown  brown  green  brown  green  blue  
[41] brown  orange yellow orange orange yellow red    orange blue   green 
[51] green  green  green  orange blue   green 
Levels: red orange yellow green blue brown

table(samp1)

samp1
   red orange yellow  green   blue  brown 
     6     18      5     15      8      4 

• Obtain our first estimate for \(p_{red}\), the true proportion of red-colors M&Ms: \(\hat{p}^{(1)}_{red} = 0.107\)

Example (cont.)

• Take second sample:

samp2 <- sample(x = obs, size = n, replace = T)
table(samp2)

samp2
   red orange yellow  green   blue  brown 
     2     18      3      7     10     16 

• \(\hat{p}^{(2)}_{red} = 0.036\)

• Repeat this process thousands of times!

• …

• After 1000 bootstrap samples, we end up with 1000 estimates for \(p_{red}\)

• Average over all estimates is \(\hat{p} _{red}= 0.091\)

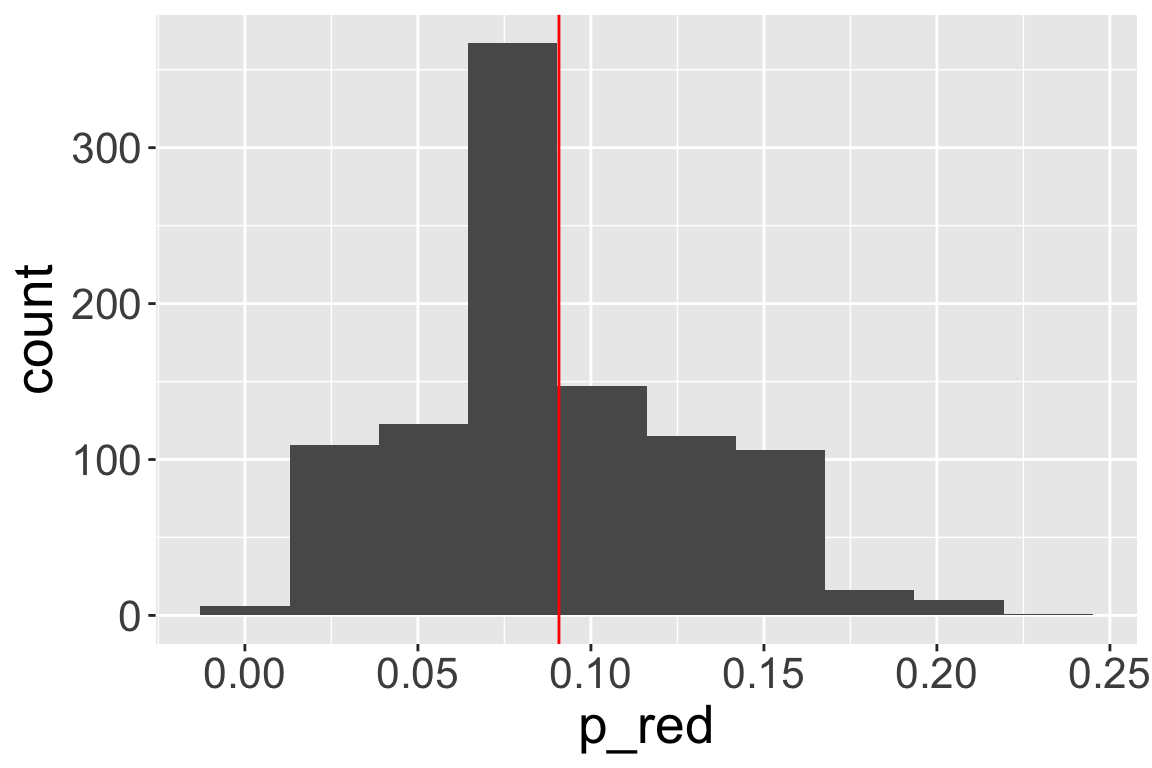
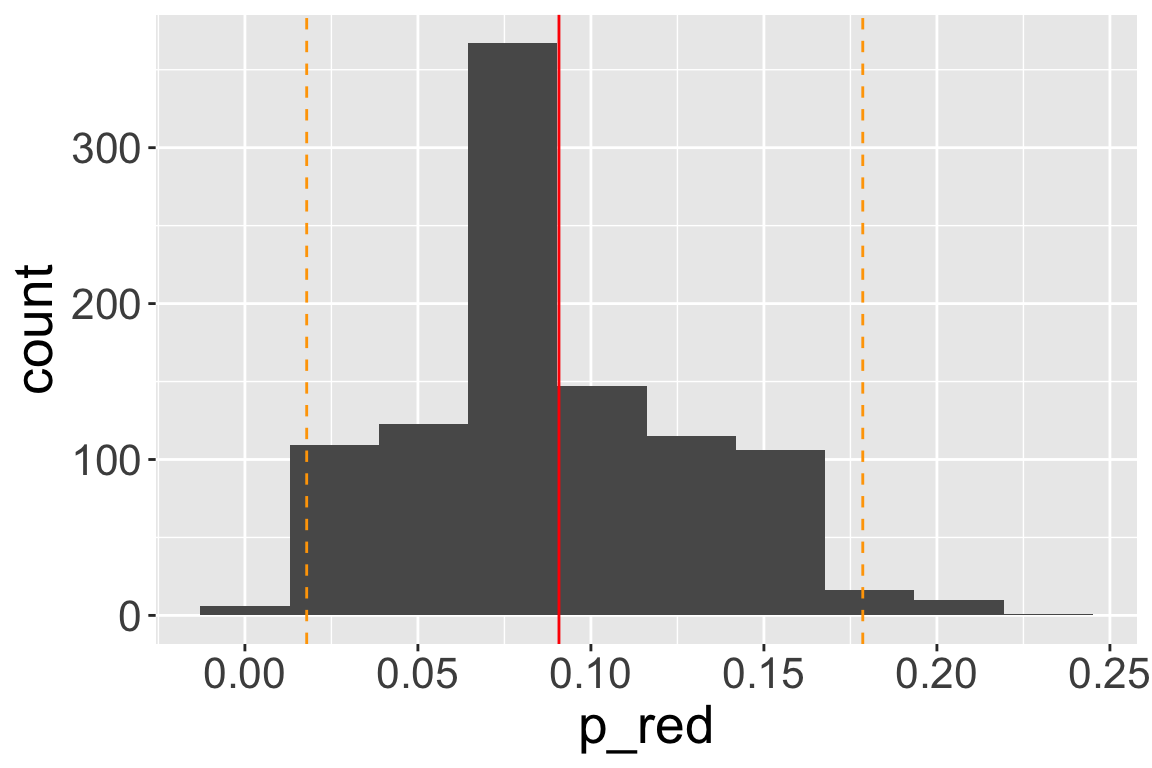
• Approximate 95% confidence interval for the proportion are the 5% and 95% quantiles of the 1000 mean estimates: (0.018, 0.179)

Comprehension checks

Suppose my original sample has the following \(n = 5\) observations: (1, 0, -2, 0.5, 4).

Which of the following are possible bootstrap samples we could obtain from the original sample?

1. (0, 0, 0, 0, 0)

2. (1, -2, -2, 3, 4)

3. (1, 0, -2, 0.5, 4)

4. (4, -2, 0)

Bootstrap: pros and cons

• Real world vs bootstrap world

• Pros:

  • No assumptions about distribution of your data
  • Very general method that allows estimating sampling distribution of almost any statistic!
  • Cost-effective

• Cons:

  • In more complex scenarios, figuring out appropriate way to bootstrap may require thought
  • Can fail in some situations
  • Relies quite heavily on the original sample