Live code:

Regression trees (pruning)

library(tidyverse)
library(vegan)
data(mite)
data(mite.env)
mite_dat <- mite.env %>%
  add_column(abundance = mite$LRUG)

Pruning in R

We will use a few more functions from the tree package to prune a large tree and obtain a “best” subtree via cost-complexity pruning and k-fold CV.

Grow large tree

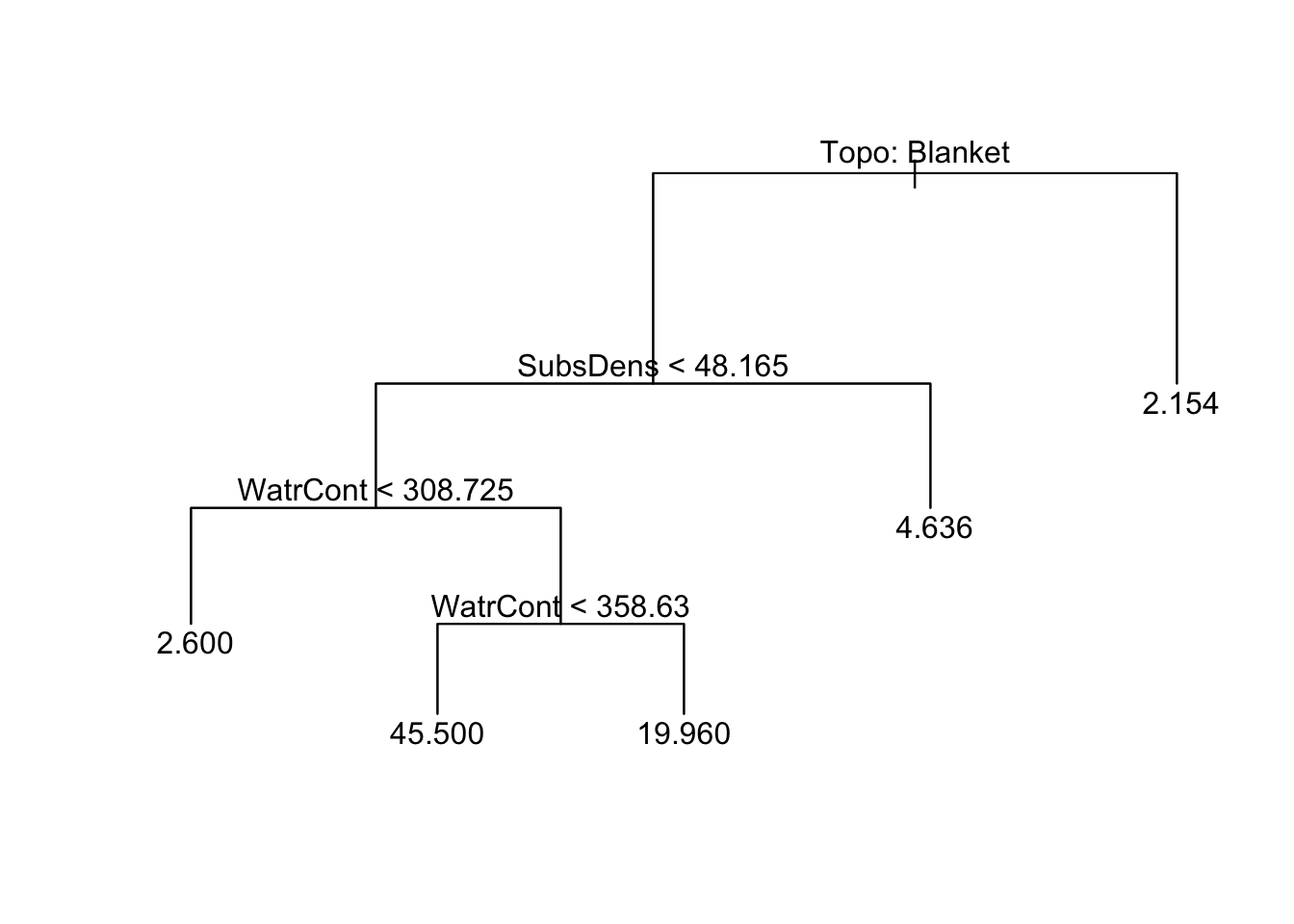
First, we will grow a large regression tree for abundance using all the predictors. Note: by default, the tree() function will grow a large tree, but will not perfectly fit the training data. It defaults to growing a tree that has at least five observations in each child node.

If we want to explicitly tell tree() to grow a larger tree, we can specify the optional argument called control. We set nobs = n (i.e. the number of training observations), and another optional control argument such as mindev, minsize, or mincut. See the help file for tree.control for more details.

Here, we will specify minsize = 2, which means that the smallest allowed node size is 2. If you view the text version of the tree, you’ll see we have many leaves where only one training observation follows a given path.

library(tree)
n <- nrow(mite_dat)
tree_mites <- tree(abundance ~ ., data = mite_dat,
                   control=tree.control(nobs = n, minsize = 2))
summary(tree_mites)

Regression tree:
tree(formula = abundance ~ ., data = mite_dat, control = tree.control(nobs = n, 
    minsize = 2))
Variables actually used in tree construction:
[1] "Topo"      "SubsDens"  "WatrCont"  "Substrate"
Number of terminal nodes:  12 
Residual mean deviance:  20.38 = 1182 / 58 
Distribution of residuals:
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
-13.210  -1.600  -1.167   0.000   1.692  10.790 

Prune the large tree

Maybe we think this tree_mites is too complex and might want to prune it to improve results. First we need to consider a bunch of candidate subtrees, then ultimately choose one single “best” tree.

Cost-complexity pruning with k-fold CV

We can use cv.tree() to perform k-fold cross-validation in order to determine the optimal level of tree complexity. This function performs cost-complexity pruning on the passed-in tree for various values of \(\alpha\). It defaults to k=10 for the k-fold CV. See the help file for more details.

Comprehension question check: why am I setting a seed?

set.seed(3) 
cv_mites <- cv.tree(tree_mites, K = 5)
cv_mites

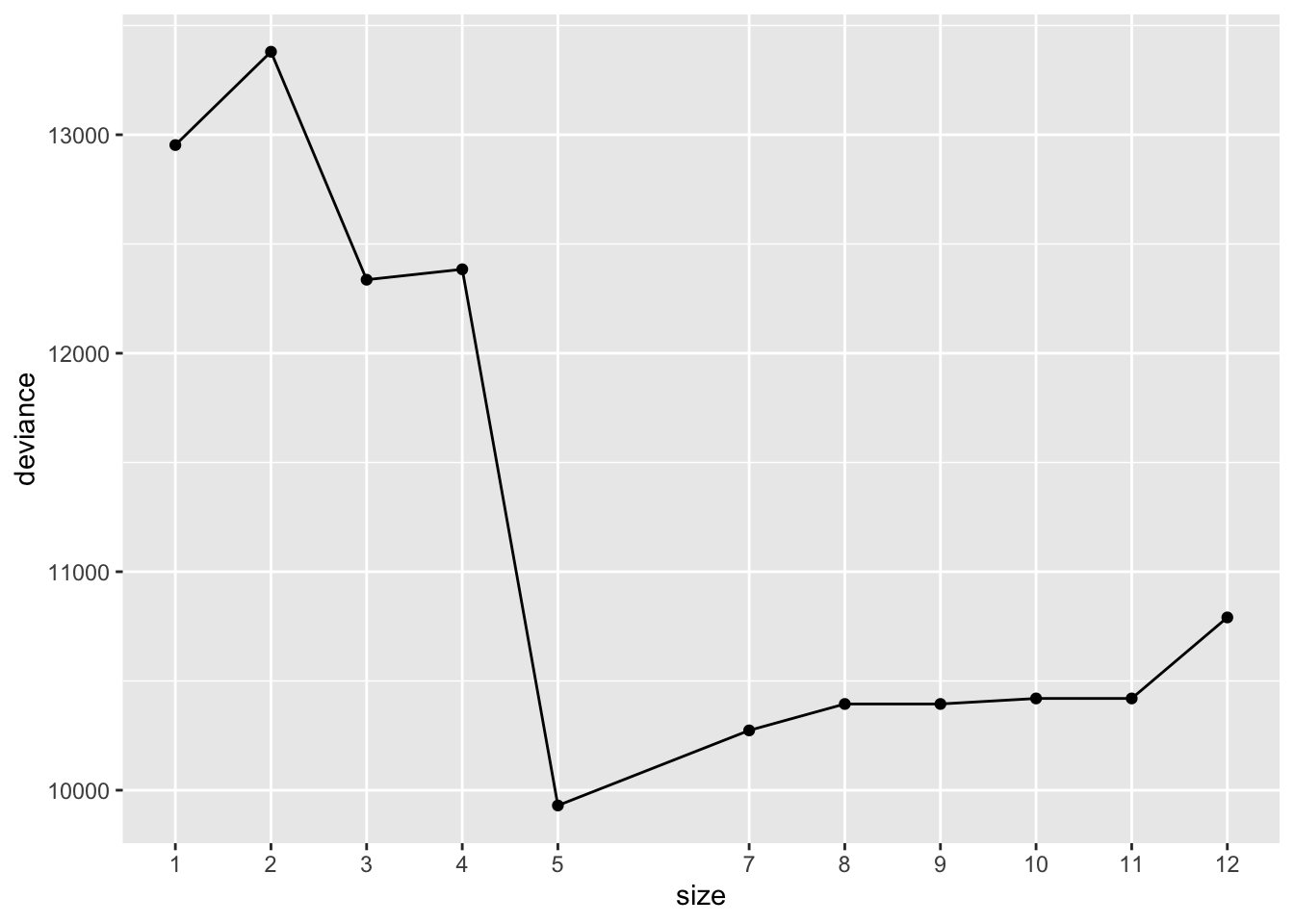
$size
 [1] 12 11 10  9  8  7  5  4  3  2  1

$dev
 [1] 10790.748 10419.939 10419.939 10394.639 10394.639 10273.679  9930.036
 [8] 12384.231 12336.495 13379.901 12952.863

$k
 [1]      -Inf  196.4455  200.1603  220.5000  264.5000  304.0513  706.3217
 [8] 1211.2527 1561.6009 1673.4848 2832.2128

$method
[1] "deviance"

attr(,"class")
[1] "prune"         "tree.sequence"

The returned output contains the cross-validated results from each sub-tree:

• size: number of terminal nodes of each tree considered
• dev: corresponding deviance of each tree
• k: value of the cost-complexity parameter used (\(\alpha\) in our notation)

We want tree with lowest deviance. Which candidate tree should we use?

best_id <- which.min(cv_mites$dev)
best_id

[1] 7

min_size <- cv_mites$size[best_id]
min_size

[1] 5

Sometimes, it’s nice to plot the CV test error as a function of \(\alpha\) (k) or the size of each subtree:

Pruning to obtain final tree

We will use prune.tree() to prune our original large tree tree_mites to the size we found from cv.tree(). Results in a much simpler tree which we could then use for predictions!

prune_mites <- prune.tree(tree_mites, best = min_size)
plot(prune_mites)
text(prune_mites, pretty = 0)